MP5: Molecules

Recursion is an important and powerful programming technique. Sometimes it is the best way to solve a problem, and sometimes it is almost the only way to solve a problem. Recursion can be tricky to wrap your head around at first, but as usual the best way to get comfortable with this technique is to practice.

For MP5 you’ll analyze molecules represented as graphs, another recursive data structure. You will use recursive and iterative functions, and apply recursive problem solving technique by breaking down a large task into several smaller ones. MP5 is the second of two Android assignments to prepare you for your final project.

MP5 is due Friday 11/16/2018 @ 5PM. To receive full credit, you must submit by this deadline. In addition, 10% of your grade on MP5 is for submitting code that earns at least 40 points by Monday 11/12/2018 @ 5PM. As usual, late submissions will be subject to the MP late submission policy.

1. Learning Objectives

MP5 gives you plenty of practice with recursive programming. You’ll work with existing data structures like you did in MP4, write member functions like you did in MP3, use collections like the arrays you used in MP2, work with strings like in MP1, and of course continue to use the imperative programming constructs introduced in MP0. It really does bring together almost everything we’ve done this semester.

The main task in MP5 is naming simple organic molecules. Writing one function to handle all molecules would be extremely hard. Fortunately, the task can be broken down into several smaller tasks that are easy to implement! Factoring out smaller, repeated pieces of functionality into helper functions is a critical skill when writing larger, more complex programs. Our test cases are designed to guide you as you build up your solution to handle more and more kinds of molecules.

2. Assignment Structure

Like MP4, MP5 is split into two modules:

/lib/: a library that performs various analyses of the given molecule. This library is the only part of the MP tested by the test suite.
/app/: an Android app for you to use for your own interactive testing. The Android app is technically functional, but could use a few modifications from you. And, for it to work correctly, you need to finish the library in lib.

Your primary job is to complete the required analyses in MoleculeAnalyzer.java. The molecule to analyze is provided for you in the form of a BondedAtom object. This data structure is recursively defined, so even though one BondedAtom instance only represents a single atom, you can use its instance methods to get references to other atoms and thereby explore the entire molecule. Every atom also has a ChemicalElement object with some information on its element, along with a variety of helper functions that we encourage you to use.

Don’t know chemistry? That’s OK! This page has thorough explanations of all the chemistry you need to know to complete the MP. Ask on the forum if you’d like any clarifications.

Your analysis functions are called by the app and, once you complete them, your app will be almost completely functional—and we’ll be happy to help you with the rest.

As always, you will find our official MP5 online documentation helpful in understanding what each function and class does.

2.1. Obtaining MP5

We are again using Android Studio for MP5.

In Android Studio, use this GitHub Classroom invitation link to fork your copy of MP5. Once your repository has been created, import it into Android Studio following our assignment Git workflow guide.

2.2. Your Goal

At this point you should be familiar with the requirements from previous MPs. For the points breakdown, see the grading description below.

3. Approaching MP5

Getting 100 points on MP5 doesn’t take a ton of code 1. But some of it is recursive code, so it will take you longer. Don’t expect to make as much progress writing recursive code when you are getting started. It’s tricky, and takes practice. Slow down and focus on applying the recursive design principles you’ve learned in lecture, lab, and on the homework problems.

3.1. Understand The Requirements

Just like with previous MPs, reading is fundamental to your success. Understand the specification, how to use lists in Java, the connections to graphs, and—particularly if you are attempting the extra credit—the chemistry tutorial. Read those first. Then read them again.

3.2. Designing Recursive Functions

Recall the guidelines for designing recursive functions that we presented in lab and lecture:

Every recursive function must have a base case. If you don’t stop recursing, you will eventually run out of memory and your program will crash. So there must be some case where you do not call yourself again.
The base case must be reached. As a corollary to the above, every set of recursive calls must eventually reach the base case. Otherwise (again) your program will recurse infinitely, run out of memory and crash.
The problem should get smaller each time. Each recursive step should reduce the size of the problem somehow. This can happen in several ways. In Fibonacci, for example, we reduce the size of the problem by reduction toward known starting values. When processing trees, we reduce the size of the problem by splitting the tree into several subtrees which are considered separately. How this happens depends on the problem, but it does need to happen somehow.

It can also be helpful to consider simple cases. How do you reverse a list with only one element? Now, extend that to a list with two elements, then three. You may begin to see a pattern emerge that helps you understand how to design your recursive approach.

3.3. Getting Help

The course staff is ready and willing to help you every step of the way! Please come to office hours, or post on the forum when you need help. You should also feel free to help each other, as long as you do not violate the academic integrity requirements.

3.4. Java `ArrayList`s

Your work on MP5 will be aided by the one of the two data structures that you meet in heaven: lists.

We’ve built a simple list together in lecture. But for MP5 you’ll want to use Java’s built-in ArrayList class, one implementation of the complete Java List interface 2.

As a review, like an array a list is an ordered collection of values. Unlike an array, a list allows you to add and remove items after it has been created. You’ll make extensive use of these list methods as you complete MP5:

add: adds a new item at the end, extending the list’s length by 1
contains: returns true if the list contains the passed value, and false otherwise
size: gets the current length of the list, just like the length field of an array

Other list methods may also come in handy. Review the official List interface documentation for the complete list and documentation.

4. Graphs

At first glance this MP may seem to be about chemistry. But it’s not. It’s really about graphs and various recursive operations on graphs.

A graph is a very general and extremely powerful data structure. It consists of a series of nodes connected by edges. Graphs can be either directed 3 or undirected 4. We can also associate properties with either the nodes or the edges of the graph.

4.1. Examples of Graphs

In this MP you’ll be working with undirected graphs where the nodes are atoms and have properties (like which element they are) and the edges are bonds between the atoms. But graphs are so ubiquitous and so powerful in computer science because of the sheer number of different things in the real world that can be represented as graphs:

Social networks are graphs, with the nodes being people and the edges friendship relationships between them. Depending on the type of social network the graph could be either undirected (accepting my friend request means that you are my friend and I am also yours) or directed (following me on Twitter does not mean that I follow you). Given the increasing importance of social networks in spreading information 5, the dynamics and properties of these networks has been a topic of intense research for years.
Many kinds of transportation problems can be modeled as graphs, with the nodes being locations (intersections, airports) and the edges paths between them (streets, air tracks). Here the edges probably have properties like distance or the amount of fuel required, and we become interested in properties of the graph like the shortest path between two points, where shortest could have multiple meanings (shortest in space, fastest, cheapest).
The internet is a graph, with the nodes being computers connected to the internet and the edges paths between them, both wired and wireless. Just like on transportation graphs, routing on the internet involves trying to determine the best path between two communicating machines.

4.2. Graph Operations for MP5

To simplify MP5, we’ve provided you with helper functions that perform the chemistry-specific naming tasks. But to get them to work, you need to complete a series of recursive functions that operate on graphs.

MP5 is set up specifically so that there is a strong mapping between the functions you need to complete and common operations on graphs. So, for example, while your getRing function locates a ring in the molecule (if one exists) because it affects the molecule’s name, this is a common graph operation: cycle detection.

Here are some of the MoleculeAnalyzer helper functions you need to complete to get full credit on MP5 6 and their analogous graph operations:

In addition, many of the other helper functions you need to compete use the results of these operations. In particular, getMolecularWeight, hasChargedAtoms, and getTips are fairly simple once you have established a list of all of the atoms in the molecule using findAllAtoms.

4.3. Recursion on Graphs

Recursion on graphs isn’t fundamentally different from recursion on trees. But there are some additional considerations to keep in mind.

Let’s consider findAllAtoms. As usual, we want to (1) identify the base case, (2) the recursive step, (3) and how we are going to combine results. Imagine we’re finding all nodes on this simple graph:

4.3.1. `findAllAtoms`: base case

On a tree we would start at the root and work our way down, but a graph doesn’t have that same notion of top and bottom. Your findAllAtoms function needs to be able to begin at any atom in the graph and locate all others 7. So instead of our base case being a leaf node, we’ll define the base case as reaching a node that we have already visited. At that point we know that some other call to our recursive function is already exploring the graph from that point and we can stop.

4.3.2. `findAllAtoms`: recursive step

On a tree we make the problem smaller by restarting our algorithm on each subtree. A graph is similar, except that we restart our algorithm on each neighbor. Like a tree, each part of the graph that begins at each of any node’s neighbors is, itself, a graph.

Note that in general this will mean that after arriving at Node 2 from Node 1 in the example above we will recursively return to Node 1. But this is fine since our base case above should realize that Node 1 has already been visited and stop at that point. This is how we ensure that the problem gets smaller at each step.

We could explicitly avoid backtracking during our recursive step by not returning to the node that we visited previously. But having the base case do this check also allows us to avoid cycles, which might cause us to return to a node that we have already visited but is not the node we came from. This is one critical difference between trees and graphs. In a tree if you start at the root and only work downward by recursing into subtrees, your recursion will always terminate. On a graph if you start at any node and continue blindly following all neighbors, your recursion will continue infinitely if the node contains a cycle or loop. The example above contains two cycles: 4 ↔ 5 ↔ 2 ↔ 3 ↔ 4 and 5 ↔ 2 ↔ 1 ↔ 5.

Given that visiting all neighbors is a common operation on graphs, we’ve helped you out by making the BondedAtom class iterable. So, given a BondedAtom current, you can visit all of its neighbors as follows:

for (BondedAtom neighbor : current) {
  // Do something with neighbor
}

4.3.3. `findAllAtoms`: combining results

Our final task is to figure out how to combine results together. Conceptually, starting with Node 1 in the example above, recursing to Node 2 will find some group of nodes while recursing to Node 5 will find another group of nodes. Then I combine them, add myself, and I’m done. But how do we get this to work in practice?

Here’s the first place where our lists are going to come in handy. findAllAtoms is already supposed to return a list of the atoms in the molecule. So to combine my results I just let all of my recursive calls modify the same list, and when they complete it will contain all of the atoms in the molecule. I can also use this list during each recursive step to check to make sure that I don’t backtrack and avoid cycles. Note that this means that I need to pass a reference to the list to each step of my recursive algorithm.

4.3.4. `findAllAtoms`: putting it all together

To help you get started with findAllAtoms, here is a solution sketch based on the solution set.

def findAllAtoms(current, atoms):
    """ if current is in atoms, we've already been here, so stop """
    """ add current to atoms """
    """ restart findAllAtoms on all current's neighbors """

Like many recursive functions, findAllAtoms is fairly beautiful and terse once you have completed it correctly. If it begins to get long and ugly, you are probably doing something wrong. Ask for help!

4.3.5. Generalizing `findAllAtoms`

findAllAtoms is a good starting point but simpler than the other recursive functions that you’ll need to complete to finish the MP. One way in which it’s simpler is that it only maintains one list. In contrast, when looking for cycles or a path between two nodes you’ll need to create a new list each time you restart your recursive function, since each neighbor establishes a new path. You’ll also need to adjust the return value of your recursive function based on what each neighbor finds.

For example, here is a solution sketch for findPath again based on the solution set:

def findPath(current, end, path):
    """ add ourselves to the path """
    """ if current equals end we're found a path, so return it """
    for neighbor in neighbors:
        """ avoid backtracking and cycles """
        """ make a copy of the path """
        """ restart findPath from the neighbor using the copied path """
        """ if a path exists from the neighbor, return it, otherwise continue """

    """ if the loop terminates then there was no path from any of my neighbors """
    """ if no path exists from any of my neighbors then no path exists from me """

Note that this algorithm only works on a graph without cycles, since once you have cycles there are multiple paths between any two nodes in the graph. Once you have findPath working you can use it is the basis for your cycle detection algorithm, which is quite similar.

5. Chemistry Tutorial

Programming is a powerful skill for many reasons, one of which is that it can be applied to virtually any science. Bioinformatics—the processing of biological data, especially genetic sequences—was critical to the Human Genome Project, for example.

In this MP, you’ll be applying your programming skills to chemistry. Nevertheless, we don’t require or expect you to have a deep background in chemistry, so this section tells you exactly what you need to know to complete the assignment 8.

5.1. Basics

All molecules are composed of multiple atoms. Every atom in a molecule has at least one bond to another atom in that same molecule. Hydrogen gas, for example, consists of two hydrogen atoms bonded to each other. In larger molecules, each atom can have multiple bonds, but each bond always connects exactly two atoms.

The number of bonds an atom makes depends on what element it is. We call the number of bonds an element wants its valence. Oxygen wants two bonds, for example. Depending on the number of electrons shared, bonds can be single, double, or triple—we’ll only concern ourselves with single and double bonds. The oxygen molecules you breathe each consist of two oxygen atoms connected to each other by a double bond, so atom is involved in exactly the number of bonds it wants to be. If an atom has more or fewer bonds than is appropriate for its valence it is considered to be charged.

Different elements have different weights—for example, a carbon atom is heavier than a hydrogen atom. All atoms of a given element have roughly 9 the same weight. You can determine the molecular weight of a molecule simply by adding up all the weights of the atoms in it.

Each element has a one- or two-letter symbol that is used to denote it in drawings and formulas. You may recognize these from the periodic table. For example, "O" is the symbol for oxygen. This MP uses only six elements: carbon, hydrogen, oxygen, fluorine, chlorine, and bromine. Those last three are all halogens—we’ll come back to that.

We’re focusing on organic molecules for this MP. All organic molecules involve carbon, generally arranged in chains with a bunch of hydrogens and sometimes a few other atoms connected to them. The simplest organic molecule is methane, one carbon atom with four hydrogen atoms connected to it by one single bond each:

  H
  |
H-C-H
  |
  H

To pass testMolecularWeight and testHasCharged you need to first complete findAllAtoms. Once you have a list of atoms you either sum their weight or return whether any atom is charged.

5.2. Drawing

The app code we’ve given you handles the drawing of molecules, but the rest of this section has illustrations of the kind of molecules we’ll ask your code to name. So you should know how to interpret these drawings.

Since organic molecules often contain a lot of hydrogen atoms and quite a few carbons, always identifying those atoms as "H" and "C" in drawings is a pain. So organic chemists use skeletal formulas to keep things tidy. Skeletal formulas never explicitly show carbon—it’s assumed that the unlabeled tips, kinks, and intersections of lines are carbon atoms. Likewise, hydrogens attached to carbon atoms are not shown—it’s assumed that every carbon has the right number of hydrogens on it to fill its valence.

So this (carbons circled in red)…

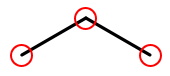
…is the same molecule as this…

  H H H
  | | |
H-C-C-C-H
  | | |
  H H H

Elements other than carbon and hydrogen are known as heteroatoms and are shown on drawings by their symbol. Hydrogens bonded directly to heteroatoms are explicitly shown on the diagram, like this:

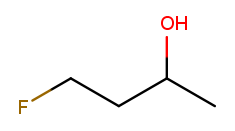
      H
      |
  H H O H
  | | | |
F-C-C-C-C-H
  | | | |
  H H H H

5.3. Intro to Naming

When talking out loud or writing in plain text, it’s not possible to draw a structure. Instead, the molecule under discussion must be named. Of course, the name needs to be descriptive enough that the molecule can be unambiguously identified. Ideally each molecule would only have one standard name. Naming things in computer science is also a challenge. There is a famous saying that there are only two hard problems in computer science: cache invalidation, naming things, and off-by-one errors.

The International Union of Pure and Applied Chemistry (IUPAC) decided the standard rules for chemical names. Since so many molecules are possible, the rules are quite extensive. We present a version of the standard that is simplified but correct for naming the molecules checked by the test cases.

Since carbon is the backbone of organic molecules, the number of carbons in the molecule sets the backbone for its name. Every chain length has a name. The names of simple carbon-or-hydrogen-only molecules always end in "ane." "Meth" is the name for a one-carbon chain, hence "methane" for the one-carbon molecule discussed above. The name for a two-carbon chain is "eth," so the molecule with two carbons fully saturated with hydrogens is "ethane." The chain base names from 1 to 10 are given in the starter code.

This is hexane, which has six carbons:

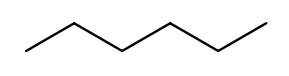
To pass testNamingSimpleStraight you only need to identify the longest chain of carbons in the molecule. Use getTips to find all tip carbons and then findPath on each pair of tips, then select the longest. Each BondedAtom has an isCarbon method that you may find useful.

5.4. Naming Rings

Chains of three atoms or more can form a cycle of bonds. A cycle of a given length is clearly not the same molecule as the straight chain of the same length, so our naming strategy needs to differentiate them. This is done by adding "cyclo" before the chain base name. The linear three-carbon chain molecule is "propane," so the three-carbon cyclic molecule is "cyclopropane."

This is cyclopentane, which has five carbons arranged in a ring:

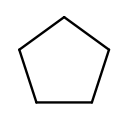
To pass testNamingSimpleCyclic, you need to complete getRing to determine whether the molecule is cyclic.

At this point you will probably need to refine your recursive approach. If you recurse down every possible bond every time, you might end up going around and around infinitely, in which case your program will crash. You’ll need to keep track of which atoms you’ve seen already using a data structure and stop once you arrive at them again.

5.5. Naming Simple Substituents

Useful molecules are usually more complex than just a chain or ring of carbons. Most organic molecules have other atoms or groups attached to the carbon backbone. For example, this is propane with a bromine bonded to the central carbon:

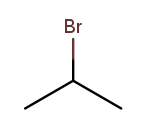
Things that are hanging off of the backbone are called substituents. To fully describe a molecule, we need to indicate not only how many carbons it has, but also which substituents it has.

Substituent names usually go before the chain base name. The name for a bromine substituent is "bromo." So we might name the previous molecule "bromopropane," but then what would we name this molecule?

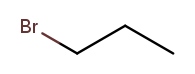
That’s also propane with a bromine attached, but in a different place! We need a way to say where the substituent is attached to the backbone. To do this, we number the carbons:

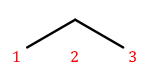
We can then name a bromine substituent on carbon 2 "2-bromo" and a bromine substituent on carbon 1 "1-bromo." Putting the name fragments together, we name the former molecule "2-bromopropane" and the latter "1-bromopropane." What about this one?

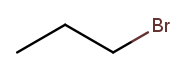
Numbering carbons from left to right, we would call this 3-bromopropane. But you can rotate the molecule in 3D space and find that it’s actually the same as 1-bromopropane. IUPAC rules prefer the name with the lowest position, so "1-bromopropane" is correct and "3-bromopropane" is not.

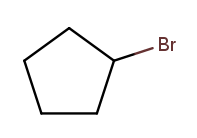
This is actually easier to deal with on a ring, since we can always number the ring carbons such that one substituent gets position 1. So this is 1-bromocyclopentane 10:

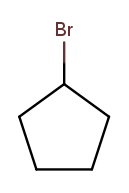
As is this:

Substituent names for other halogens are similar. Fluorine is "fluoro," chlorine is "chloro."

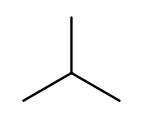
It’s possible for the carbon chain to branch, and when that happens we get carbon (alkyl) substituents. These are named similarly to straight chains, but suffixed with "yl" instead of "ane." A single-carbon ("meth") branch is called a "methyl" substituent, so this is 2-methylpropane:

Since the base name for a two-carbon chain is "eth," one might name this "2-ethylpropane" because it has a three-carbon backbone with a two-carbon branch:

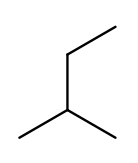
But if we rotate things a bit, it becomes a four-carbon backbone with a one-carbon branch (2-methylbutane):

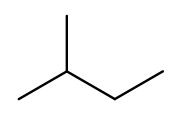
IUPAC rules prefer the longer backbone, so "2-methylbutane" is correct. "2-ethylpropane" is incorrect (because it has a shorter backbone), as is "3-methylbutane" (because it has a higher substituent position).

Again, this is actually easier on rings, since we’re always going to consider the cycle the backbone. This molecule has a cycle of three carbons ("cyclopropane") with a three-carbon branch substituent ("propyl"), so we name it "1-propylcyclopropane":

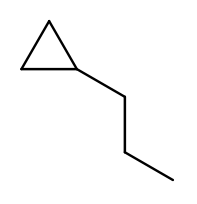
To pass testNamingOneSubstituentCyclic, you need to find any ring present (using getRing) and then rotate it properly so that the substituent is located at position 1 on the ring (using rotateRing).

To pass testNamingOneSubstituentLinear, you need to select the longest backbone that places the substituent in the lowest numbered position. Note that you should consider backbones running in either direction.

Here is a strategy to find the correct backbone and direction:

Identify all the tip carbons, which are bonded to at most one other carbon atom
For each tip carbon, recursively find all paths through the molecule starting at that carbon
- Your recursive function will probably take the last carbon visited, the path taken so far, and the list in which to store complete paths.
- At every carbon, recurse into all the attached carbons that aren’t the one previously visited, extending the path taken so far
- If another tip has been reached, add the now-finished path to the list of complete paths
Select the longest carbon chain from the list of complete paths—this is the backbone
Find the substituent, if present
If the substituent’s position is closer to the high-numbered end of the chain than to the beginning, reverse the list of backbone carbons

Any carbon atom not in the list of backbone carbons is part of an alkyl substituent. When exploring alkyl substituent chains to find their length, you must be careful to avoid recursing back into the backbone.

5.6. High-Priority Substituents

All the substituents discussed above are named before the backbone in the final, overall name. They are considered low-priority substituents. There are also high-priority substituents whose presence affects the suffix of the overall name. These include alcohols, ketones, aldehydes, and carboxylic acids.

An alcohol substituent is an OH (oxygen and hydrogen) group attached to the backbone by a single bond, like in this molecule 11:

  H H
  | |
H-C-C-O-H
  | |
  H H

This is the skeletal drawing of the same molecule:

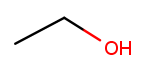
It has two carbons, so the backbone name is "eth." The substituent can be at position 1 if we number from right to left. Alcohol substituents change the suffix of the name from "ane" to "anol," with the substituent position inserted before the "ol." So we would name that molecule ethan-1-ol 12.

Likewise, this molecule has a five-carbon backbone ("pent") and an alcohol substituent at position 2, so we name it pentan-2-ol:

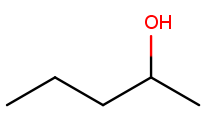
Ketone substituents are oxygen atoms double-bonded to the backbone. They change the suffix to "anone," again with the position before the "one." This molecule removes fingernail polish:

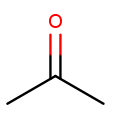
It has a three-carbon backbone ("prop") and a ketone substituent at position 2, so its systematic name is propan-2-one.

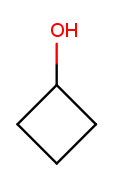
Alcohols and ketones can both appear on rings too. This is cyclobutan-1-ol (cyclic four-carbon backbone with an alcohol substituent):

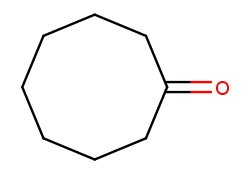
And this is cyclooctan-1-one (cyclic eight-carbon backbone with a ketone substituent):

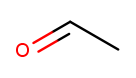
The other two kinds of high-priority substituents we consider can only appear at the tip of a linear molecule. We’ll refer to them collectively as end groups. Since they can only occur on tips, they are always assigned position 1, so that does not need to be made explicit in the name. Aldehydes are essentially ketones that happen to be at a tip 13. They are named similarly to alcohols, but with "al" instead of "ol" on the end. This molecule has a two-carbon backbone ("eth") and an aldehyde tip ("al"), so we name it ethanal:

To identify aldehydes, notice that the tip carbon is double-bonded to an oxygen and single-bonded to at least one hydrogen.

Carboxylic acids are essentially a combination of an aldehyde and an alcohol on one tip carbon. They replace the "ane" suffix with "anoic acid." So the three-carbon carboxylic acid is named "propanoic acid":

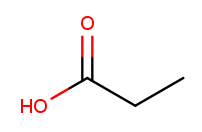
To identify carboxylic acids, notice that the tip carbon is double-bonded to one oxygen and single-bonded to another.

Note that we have provided code to handle suffix-altering substituents as described above, so there is nothing extra for you to do here. Move on to the extra credit if you want an additional challenge!

You now know all the naming rules you need to get 100 points on MP5. But you can earn a total of 10 points of extra credit by handling more interesting cases! Note that these points do not come easy. But if you are up for the challenge, read on to learn more.

5.7. Multiple Substituents

Challenge problem! You can earn 5 points of extra credit for handling this case.

A lot of useful molecules have multiple substituents, not just one. To fully describe these, we need to include information about each substituent in the name. To do that, we name each substituent by itself, then put all the name fragments together. Consider this three-carbon molecule:

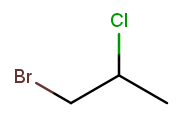
To minimize the position number of the first substituent encountered, we number from left to right. We then have a bromine at position 1 ("1-bromo") and a chlorine at position 2 ("2-chloro"). The carbon backbone’s name is "propane," so we put it all together, separate substituent fragments with an extra dash, and get 1-bromo-2-chloropropane. Note the lack of dash between the last substituent fragment and the backbone name.

Now let’s swap the halogens:

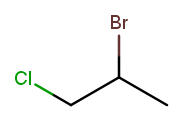
The molecule is still numbered from left to right, so one might name it 1-chloro-2-bromopropane. But the correct name is 2-bromo-1-chloropropane—IUPAC rules order substituents alphabetically by name, not numerically by position.

Now let’s make both the halogens chlorine:

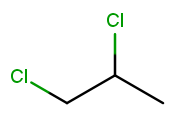
When there are multiple substituents with the same name (but not necessarily position), we combine them into one name fragment by putting all the positions into one sorted comma-separated list and adding a multiplicity prefix indicating the number of copies of the substituent. Since this molecule has chlorine at positions 1 and 2, the position list is "1,2". Since there are two instances of the chlorine substituent, we prefix the "chloro" with "di." (Three is "tri" and so on; the starter code contains an array with all the multiplicity names.) The full name for this molecule is 1,2-dichloropropane.

It’s possible to have multiple substituents at the same position:

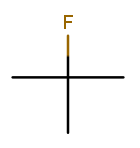
That’s 2-fluoro-2-methylpropane because the (top) fluorine substituent and the (bottom) methyl substituent are both on position 2 of the (horizontal) backbone. Notice that the "fluoro" part is first because F sorts before M.

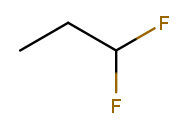
If the same substituent occurs multiple times on the same carbon, the position number appears multiple times in the list. So this is 1,1-difluoropropane:

The multiplicity prefixes do not affect the sorting of the substituent names. Consider this molecule:

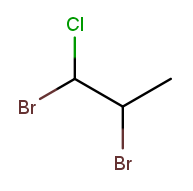
It has bromine ("bromo") substituents at position 1 and 2, plus a chlorine ("chloro") substituent at position 1. So the bromine part of the name is "1,2-dibromo" and the chlorine part is "1-chloro." The prefix "di" in "dibromo" doesn’t count for substituent sorting, so B sorts before C and the full name is 1,2-dibromo-1-chloropropane.

There can also be multiple high-priority substituents. Just like with low-priority ones, all the positions at which the substituent occurs go into the comma-separated list and the multiplicity prefix is added to the substituent name. Consider this four-carbon chain with two alcohols:

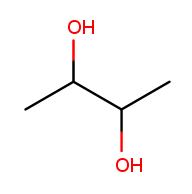
Alcohol substituents occur at positions 2 and 3, and there are two of them, so the name will end in "-2,3-diol." Since the fragment after the last dash begins with a consonant, however, the "e" in "ane" is retained (to make the name easier to pronounce). So the name is butane-2,3-diol, not butan-2,3-diol.

The prefixes for high multiplicities, like "tetra" for four, tend to end with "a." When the last fragment starts with "o," the multiplicity’s "a" is cut off to make the name easier to pronounce. So this is propane-1,1,3,3-tetrol, not propane-1,1,3,3-tetraol:

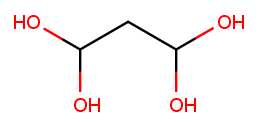
To pass testNamingMultipleSubstituents, you need to find the best backbone (whether linear or cyclic), numbered in a way that minimizes the position of the first substituent encountered. If you haven’t implemented rotateRing yet, you should do that now. You may also need to refine your getLinearBackbone helper function.

This test case does not involve end groups. The molecules you’re asked to name here have either low-priority or high-priority substituents, not a mix of both.

You now know enough naming rules to get 5 extra credit points on MP5! You can earn 5 more by handling even more tricky cases.

5.8. Priority Tiebreaks

Challenge problem! You can earn 5 points of extra credit (on top of the previous 5) for handling this case.

Up to this point, it’s been fairly easy to choose the correct numbering direction once the backbone is established—either the molecule was symmetric or one direction encounters a substituent before the other. All substituents in each tested molecule had the same priority. Now it’s time for the idea of priority to actually make a difference. How do we number this molecule?

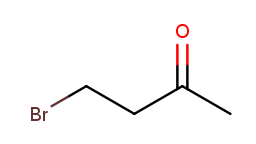
If we go from left to right, the bromine gets position 1 and the ketone gets position 3. That sounds good. But the ketone is a high-priority substituent, so its position is more important to minimize. The correct numbering direction is from right to left, so the name is 4-bromobutan-2-one ("but" from the four-carbon backbone, "2-one" from the ketone at position 2, and "4-bromo" from the bromine at position 4).

Likewise, if there are any high-priority substituents on a ring, one should occupy position 1:

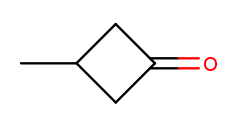
That molecule is named 3-methylcyclobutan-1-one because numbering starts at the rightmost carbon.

High-priority substituents also affect the selection of the backbone in non-cyclic molecules. Previously this molecule would be expected to have a five-carbon backbone:

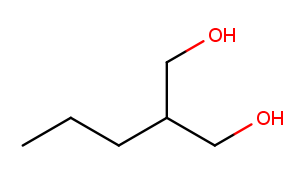
But (our simplified version of) IUPAC rules say that all high-priority substituents must be attached to the backbone. So that molecule’s backbone is the three carbons between the alcohol substituents, and the three-carbon chain going off to the left is a "propyl" substituent. This molecule’s name is 2-propylpropane-1,3-diol.

To break ties between possible backbones of the same length after ensuring that all high-priority substituents are included, compare the total number of substituents:

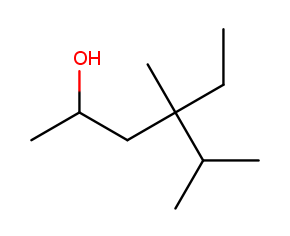
The four-way branch carbon and the three carbons to its left are definitely included in the backbone because the alcohol is attached over there. If the backbone continued to the right, the methyl and the fork below would each be substituents. But if the backbone continued down, the methyl above, ethyl to the right, and methyl off the three-way branch are each a substituent. That way produces more substituents and is the correct backbone. It is numbered from left to right because that direction encounters an alcohol at position 2, while the other way only encounters a methyl at position 2.

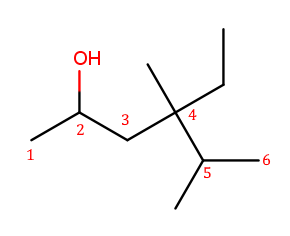
Above is the correctly numbered backbone. The full name is 4-ethyl-4,5-dimethylhexan-2-ol.

Notice how the previous example used position 2 as the direction tiebreak because both directions had no substituents on backbone carbon 1. Comparisons continue until the tie is broken. Consider this nearly symmetric molecule:

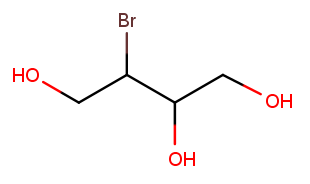
Either direction has a high-priority substituent at position 1. Right-to-left has a high-priority substituent at position 2, but left-to-right has only a low-priority substituent there. So right-to-left wins, and the correct name is 3-bromobutane-1,2,4-triol.

The presence of multiple substituents on the same carbon can also serve as a tiebreak:

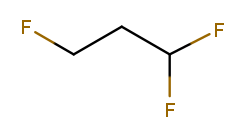
Numbering left to right produces one fluorine at position 1, while going right to left produces two at position 1. So right-to-left wins, and the correct name is 1,1,3-trifluoropropane. One high-priority substituent beats any number of low-priority ones, so if the leftmost fluorine was replaced with an alcohol, the numbering would go left to right.

If the count of substituents of both priorities is the same at every backbone carbon, the final tiebreak is the name of the substituent—alphabetically first wins:

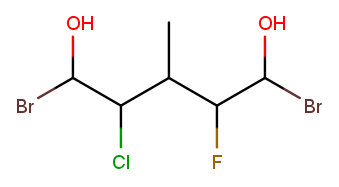
Both directions have a high-priority substituent at positions 1 and 5 and low-priority substituents at positions 2, 3, and 4. The substituents are exactly the same at position 1, so tiebreak proceeds to position 2. Left-to-right has "chloro" where right-to-left has "fluoro." "Chloro" is first alphabetically, so left-to-right wins: the name is 1,5-dibromo-2-chloro-4-fluoro-3-methylpentane-1,5-diol.

All these rules are the same for cyclic molecules. This molecule should be numbered starting at the rightmost carbon and going clockwise:

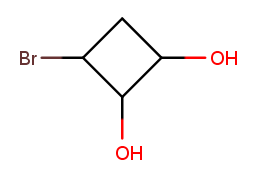
That way, it has high-priority substituents at positions 1 and 2, plus a low-priority one at position 3. Starting at the bromine would put a low-priority substituent at position 1 instead. Starting anywhere else would visit the top (substituent-less) carbon before getting to all the substituted ones.

On rings, the alphabetic tiebreak affects the starting point in addition to the numbering:

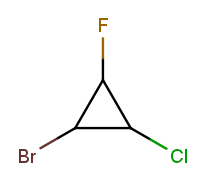
All six possible numberings have one low-priority substituent at each of the three positions. The best one puts the alphabetically first substituent in position 1 and the alphabetically next one in position 2. The correct numbering starts at the bromine and goes counterclockwise, naming the molecule 1-bromo-2-chloro-3-fluorocyclopropane.

In summary, our rules break backbone and direction ties in this order:

Has all high-priority substituents directly attached
Longest carbon chain
Highest number of total substituents
Highest number of high-priority substituents at each position (from 1 until tiebreak)
Highest number of any substituents at each position (from 1 until tiebreak)
Alphabetically by substituent name (from 1 until tiebreak, remember that each position can have multiple substituents!)

A good strategy is to generate a list of candidate backbones/numberings and filter that down by comparing two at a time.

To pass testNamingPriority, you will need to further refine getLinearBackbone and getRing. In particular, getRing will need the ability to flip the ring, causing it to be numbered in the opposite direction. Take full advantage of the convenience methods on BondedAtom—they’re all there for a reason.

You now know all the naming rules you need to get 110 points on MP5! None of the molecules we ask you to name have multiple different types of high-priority substituents, since that requires new rules.

6. Grading

As always, 100 points is full credit on the MP. But in MP5, there are 110 points available, broken down as follows:

10 points for computing molecular weight (getMolecularWeight), which requires implementing findAllAtoms
10 points for determining whether the molecule has any charged atoms (hasChargedAtoms), which also requires implementing findAllAtoms
70 points for naming: (getIupacName)
- Note that while all the test cases below test this single function, they test increasingly complex cases
- 20 points for cyclic (ring) molecules with no substituents, which requires findRing
- 20 points for linear (straight-chain) molecules with no branching or substituents, which requires implementing findPath and getLinearBackbone
- 10 points for cyclic molecules with exactly one substituent that does not affect the suffix of the name, which requires implementing rotateRing
- 10 points for linear molecules with exactly one substituent that does not affect the suffix of the name (but that may be a branch), which requires refining getLinearBackbone
- 5 points for molecules with multiple substituents, some of which may be different, but where no priority tiebreaks are required—this is extra credit
- 5 points for molecules with multiple substituents where priority tiebreaks are required—this is very hard extra credit 14
10 points for no checkstyle violations
10 points for pushing code that earns at least 40 points before Monday 11/12/2018 @ 5PM

6.1. Test Cases

As in previous MPs, we have provided exhaustive test cases for each part of MP5. Please review the MP0 testing instructions.

6.2. Chemical Formulas

The getFormula function is not tested by the test suite, but can be used by the app. Since it is not graded, you may implement this function using any formula format that you like. The reference solution uses the Hill system, in which (for example) methane’s formula is CH4 and ethanol’s is C2H6O. If you’re feeling adventurous, you might try generating condensed structural formulas.

7. Submitting Your Work

Follow the instructions from the submitting portion of the CS 125 workflow.

And remember, you must submit something that earns 40 points before Monday 11/12/2018 @ 5PM to earn your 10 early deadline points.

7.1. Academic Integrity

Please review the syllabus academic integrity section.

If you cheat on MP5, we will treat your CS 125 grade with a strong reducing agent.